About
Tao Zhang is a soft-matter/biophysics theorist. He is interested in designing novel soft-matter materials with computational modeling. He is also interested in building physical models for biological systems using both analytical analysis and numerical simulations.
- Theoretical Soft-Matter/Biophysics
- Soft Materials - Hydrogels / Polymer Nanocomposites
Ph.D. in Physics, 2015
Syracuse University
B.S. in Physics, 2010
University of Science and Technology of China
Experience
Publications
Projects
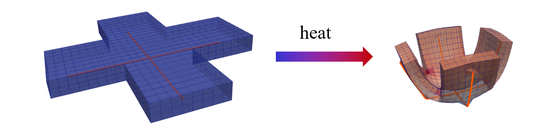
Fibers on Surface of Thermo-responsive Gels
We pattern the outer layers of thin, thermo-responsive gels with elastic fibers to induce 3D shape changes.
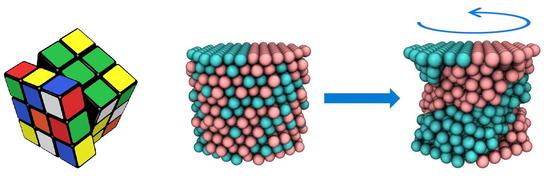
Using Torsion for Controllable Reconfiguration of Binary Nanoparticle Networks
We take inspiration from the early Rubik’s cube to design an analogous mechano-responsive system. We focus on polymer-grafted nanoparticles (PGNs), where each rigid nanoparticle core is decorated with a corona of polymer chains. The free ends of these chains encompass reactive functional groups that allow the polymers to form “arms” between neighboring particles and thus, interconnect the PGNs into a network. In effect, these polymer arms act as the elastic bands and the nanoparticles correspond to the individual blocks in the toy. Using computational modeling, we show that by applying torsion to this material, we can achieve significant control over the arrangement of a binary mixture of nanoparticles and hence, tailor the nanostructure of the composite.
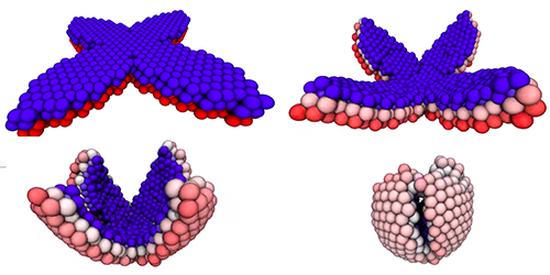
Shape-Shifting Droplet Networks
Taking a cue from biology, researchers have engineered materials that, through self-assembly, fold into designated geometries. Recent work showed that sheets of aqueous droplets can assemble into a variety of three-dimensional shapes. Expanding on this result, Mark Bowick and collaborators at Syracuse University, have now demonstrated theoretically that such droplet networks can be programmed to reversibly switch between different shapes. This finding is a step toward biologically inspired robots that can change their shape according to their environment.
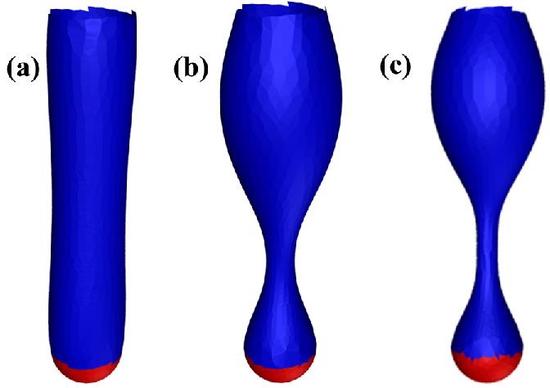
Endocytosis in Yeast
We have constructed a theoretical model of endocytosis in yeast. Recent experiments on endocytosis in yeast demonstrate that the actin cytoskeleton plays a crucial role in the deformation of the cell membrane. However, competing ideas remain as to precisely how the actin cytoskeleton organizes itself to help drive the deformation. To begin to resolve this controversy, we mathematically model clathrin-mediated endocytosis in yeast using variational methods and Monte Carlo simulations. Our results also suggest that the pinch-off mechanism may be assisted by a pearling-like instability.
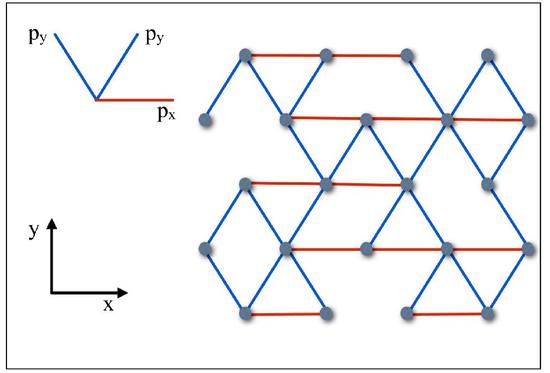
Mechanics of Anisotropic Spring Networks
The actin cytoskeleton gives the cell shape and support, is crucial for cell locomotion, and participates in cell division. To study the mechanical properties of the actin cytoskeleton as modeled by rigidity percolation (disordered spring networks), we have analytically and numerically studied disordered spring networks with an underlying anisotropy, i.e. where the filaments are preferentially oriented along one direction. We found, for example, that the increasing the anisotropy, increases the filament density required for a nonzero shear modulus (rigidity).
Talks
Contact
- zhangtao.scholar@sjtu.edu.cn
- 800 Dongchuan RD. Minhang District, Shanghai, China